Linear Controls

Contents

• Linear systems
  • Asymptotically stable system
  • Unstable System
  • Marginally Stable System
  • Stable system (with negative real part complex eigenvalues)
  • Stable system (with negative real part complex eigenvalues)

Linear Systems

The systems considered are continuous linear time invariant autonomous systems.

The solution to the above system being,

In what follows, I present systems with different initial conditions i.e, \(x(t_0)\) for various eigenvalues.

Asymptotically stable system

$A = \begin{bmatrix} -.5 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -3 \\ \end{bmatrix}$

The above system has eigenvalues (-0.5,0), (-2,0), (-3,0).

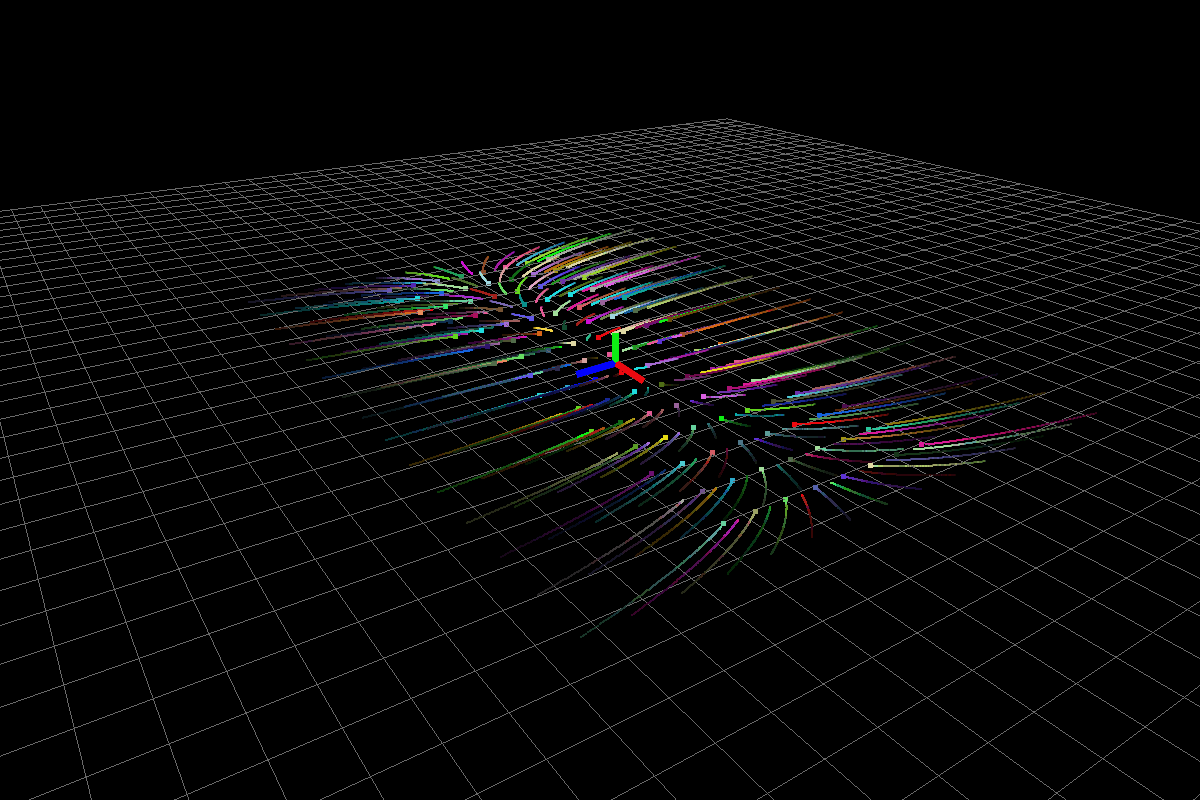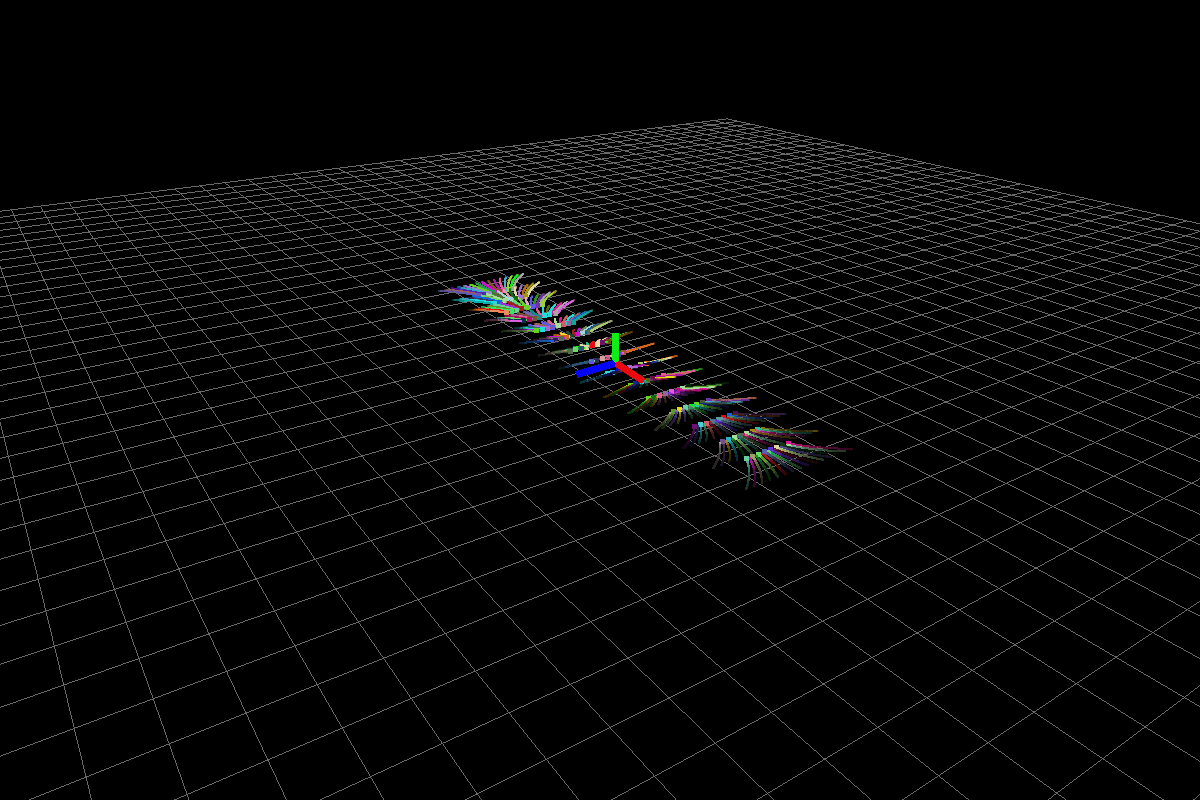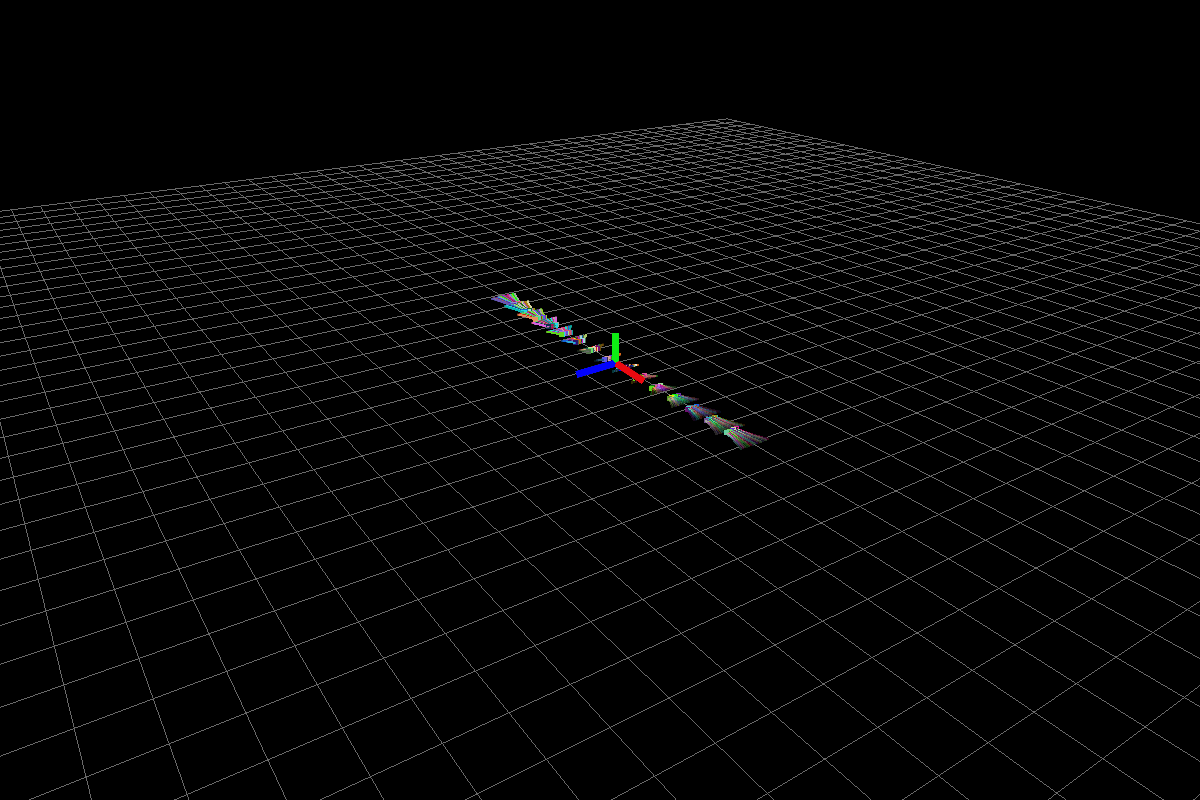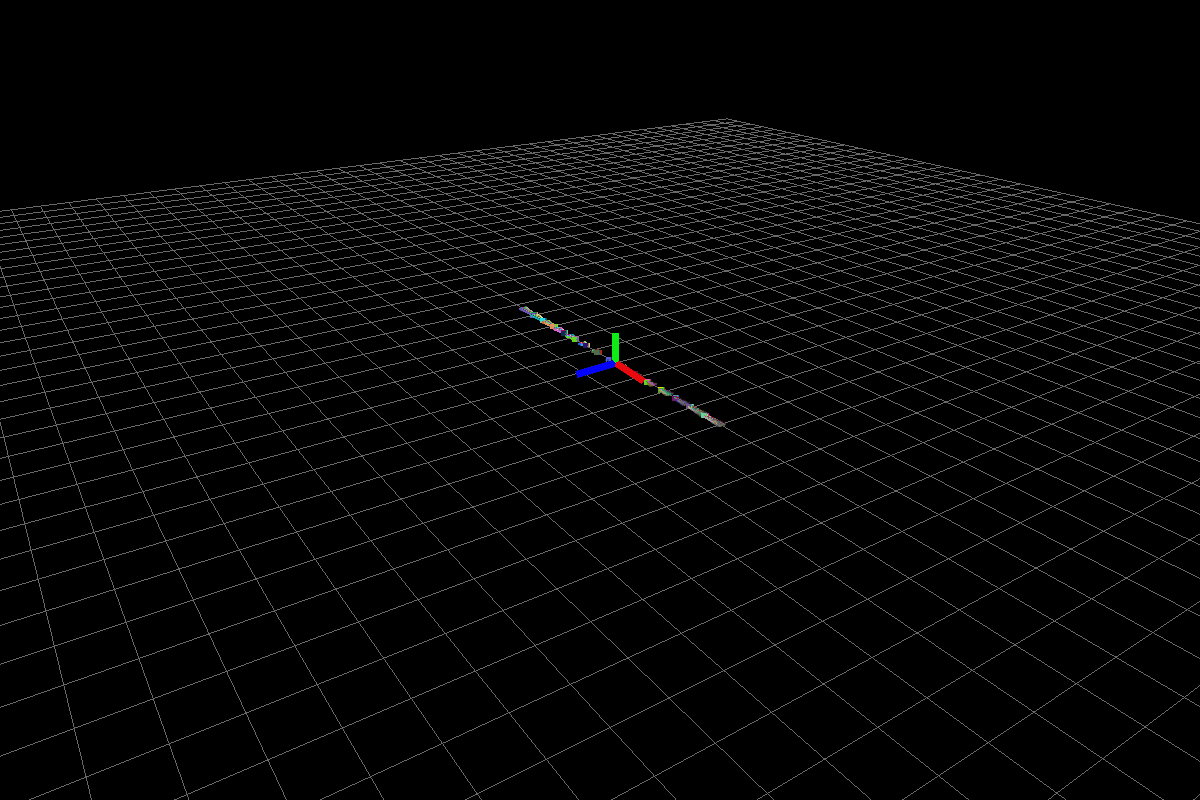Fig0: Stable system.

Unstable system

$A = \begin{bmatrix} -1 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 0 & 0.5 \\ \end{bmatrix}$

The above system has eigenvalues (-1,0), (-2,0), (0.5,0). Because of positivity of third eigenvalue, all the particles shoot to infinity exponentially fast.

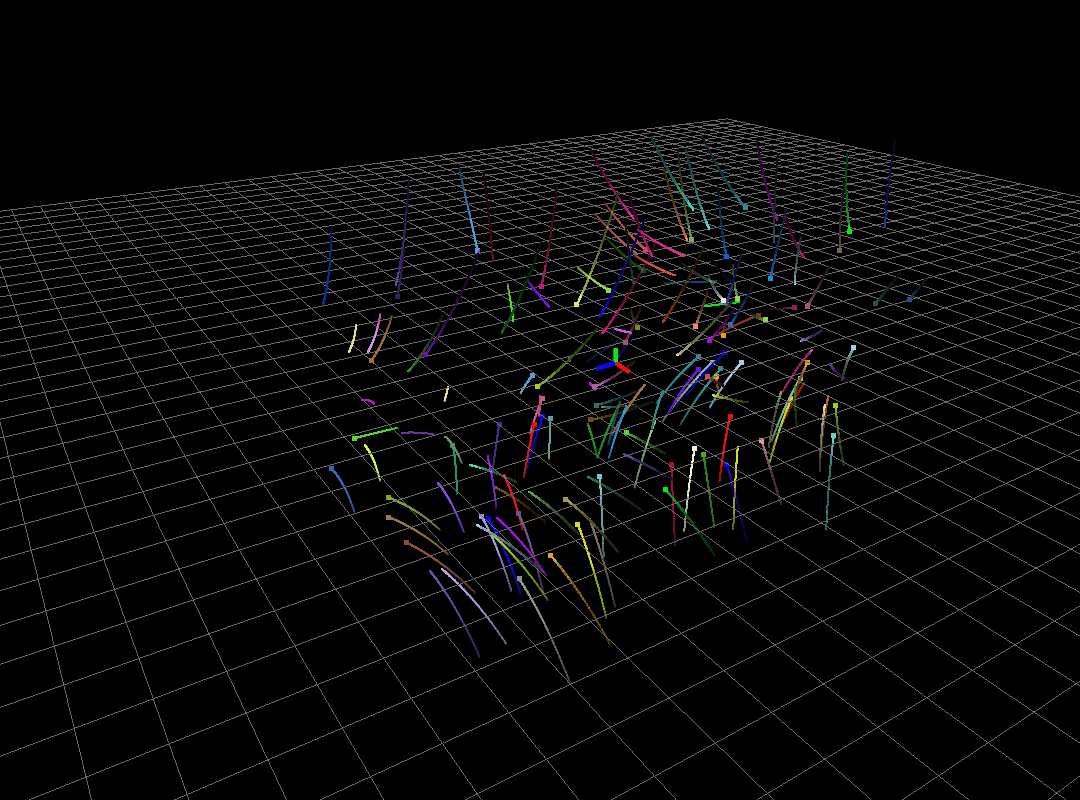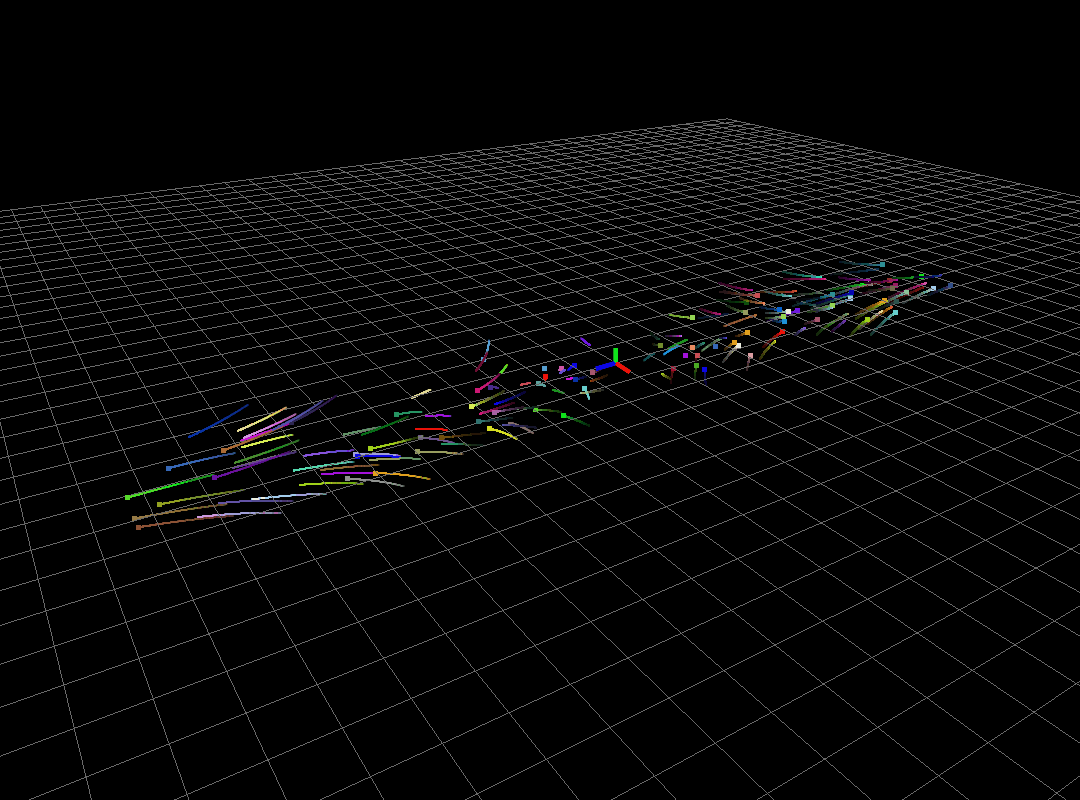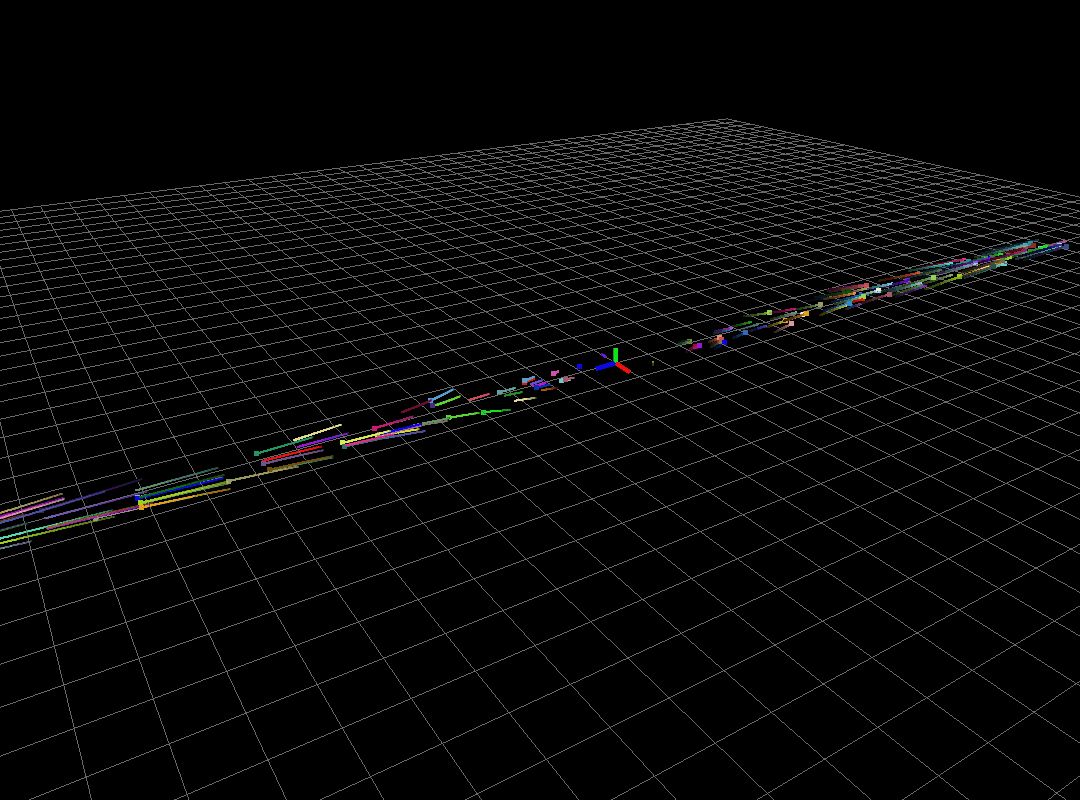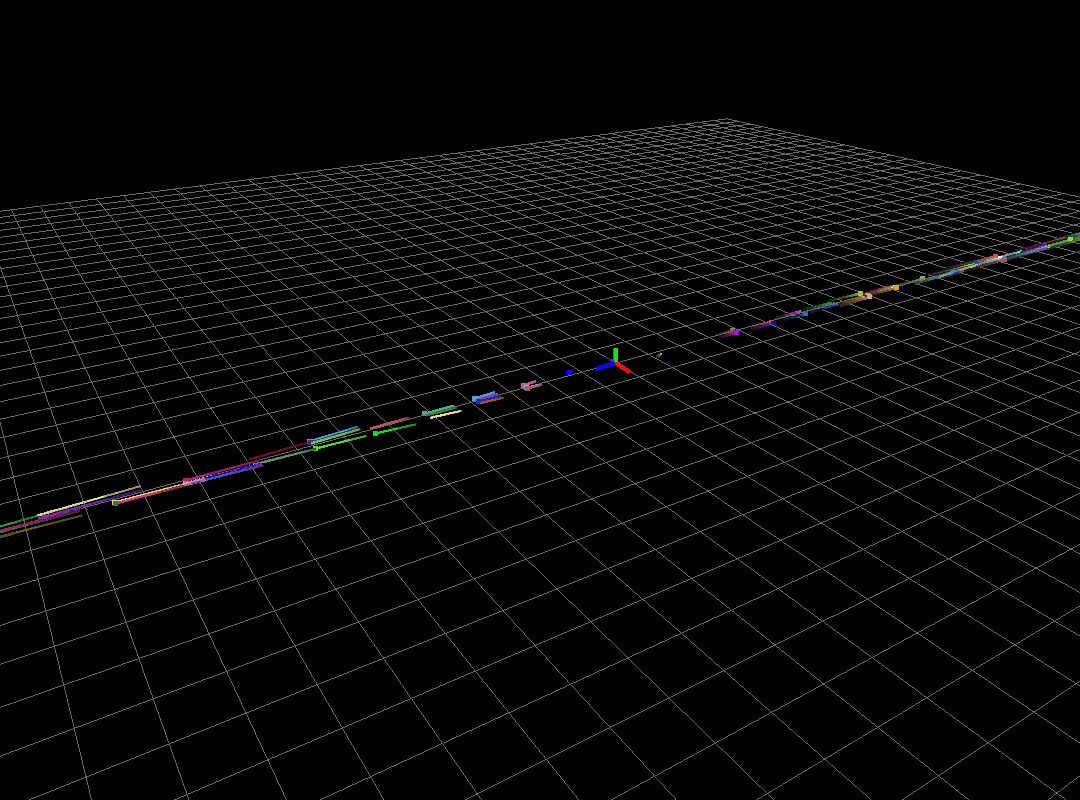Fig1: Unstable system.

Marginally stable system

$A = \begin{bmatrix} -2 & 0 & 0 \\ 0 & 0 & -2 \\ 0 & 2 & 0 \\ \end{bmatrix}$

The above system has eigenvalues (-2,0), (0,2), (0,-2). Because of real part being zero for third eigenvalue, \(\lvert \lvert x(t)\rvert \rvert \) is bounded but the system is not asymptotically stable.

Fig2: Marginally stable system.

Stable system (with negative real part complex eigenvalues)

$A = \begin{bmatrix} 0 & -2 & 0 \\ 2 & 0 & -2 \\ 0 & 2 & -2 \\ \end{bmatrix}$

The above system has eigenvalues (-0.43016,2.61428) (-0.43016,-2.61428) (-1.13968,0).

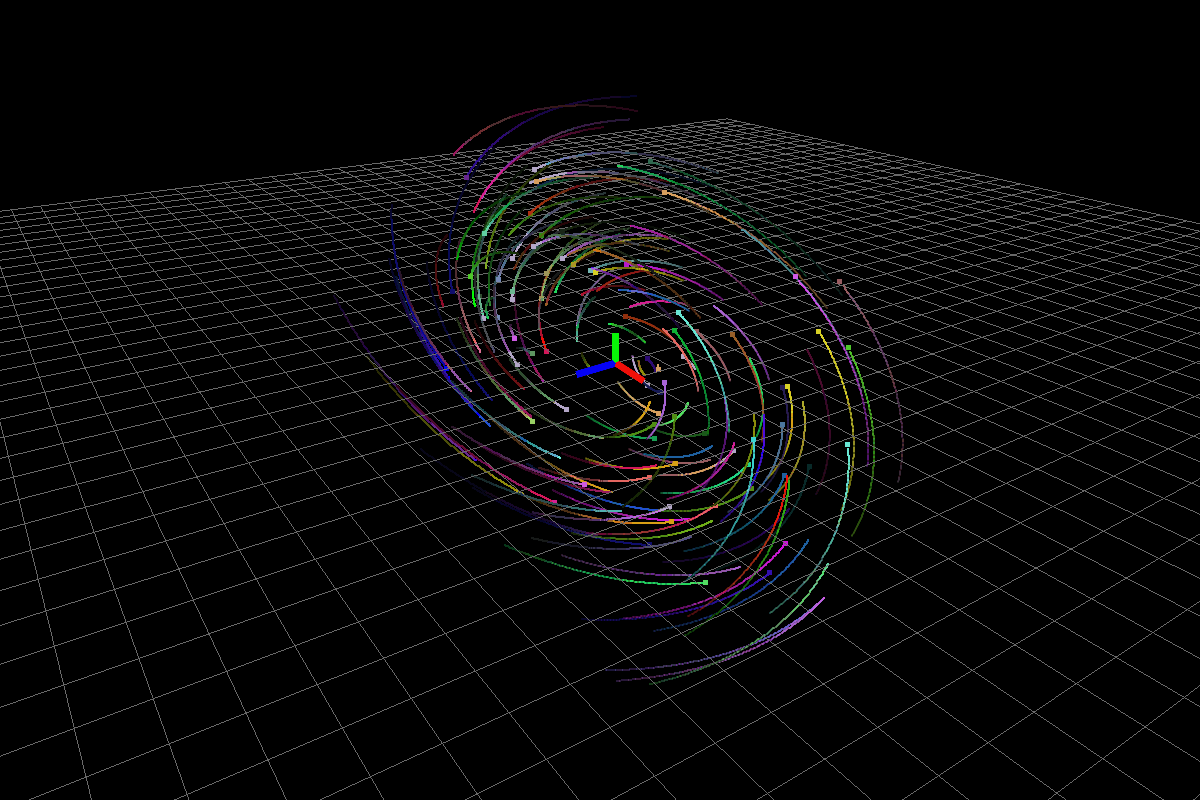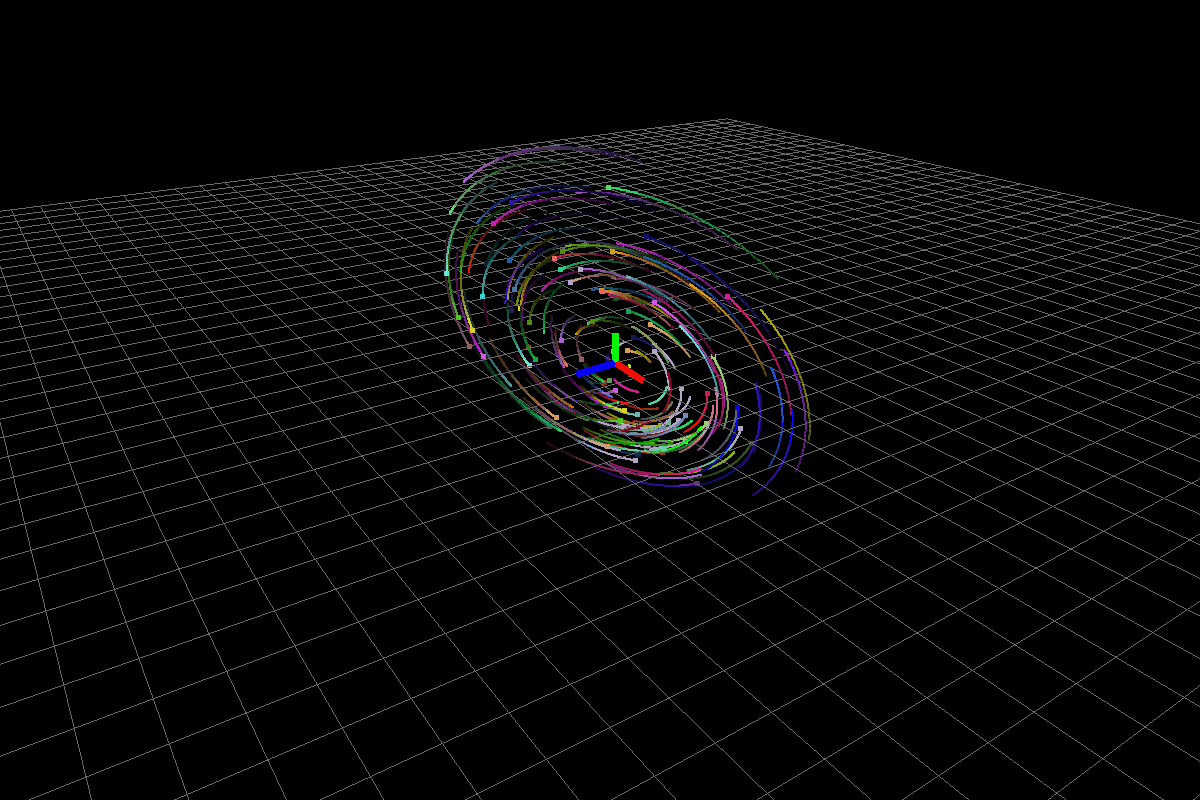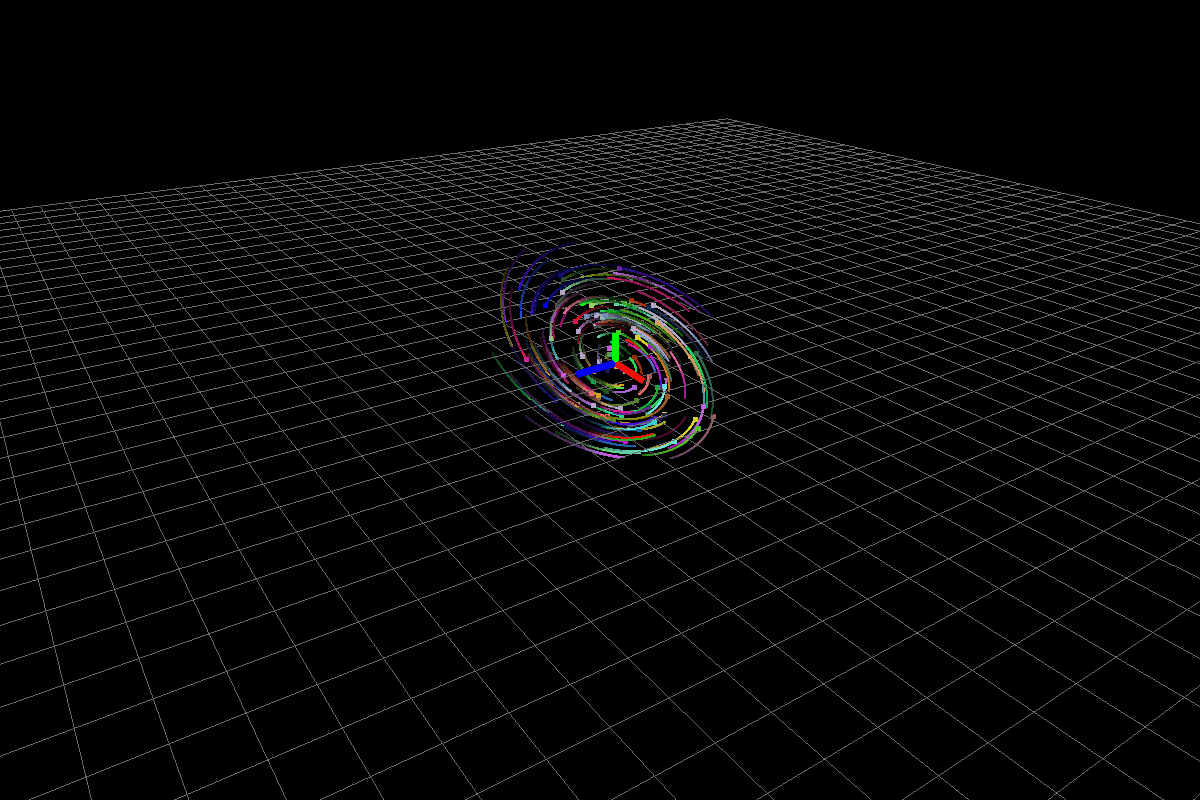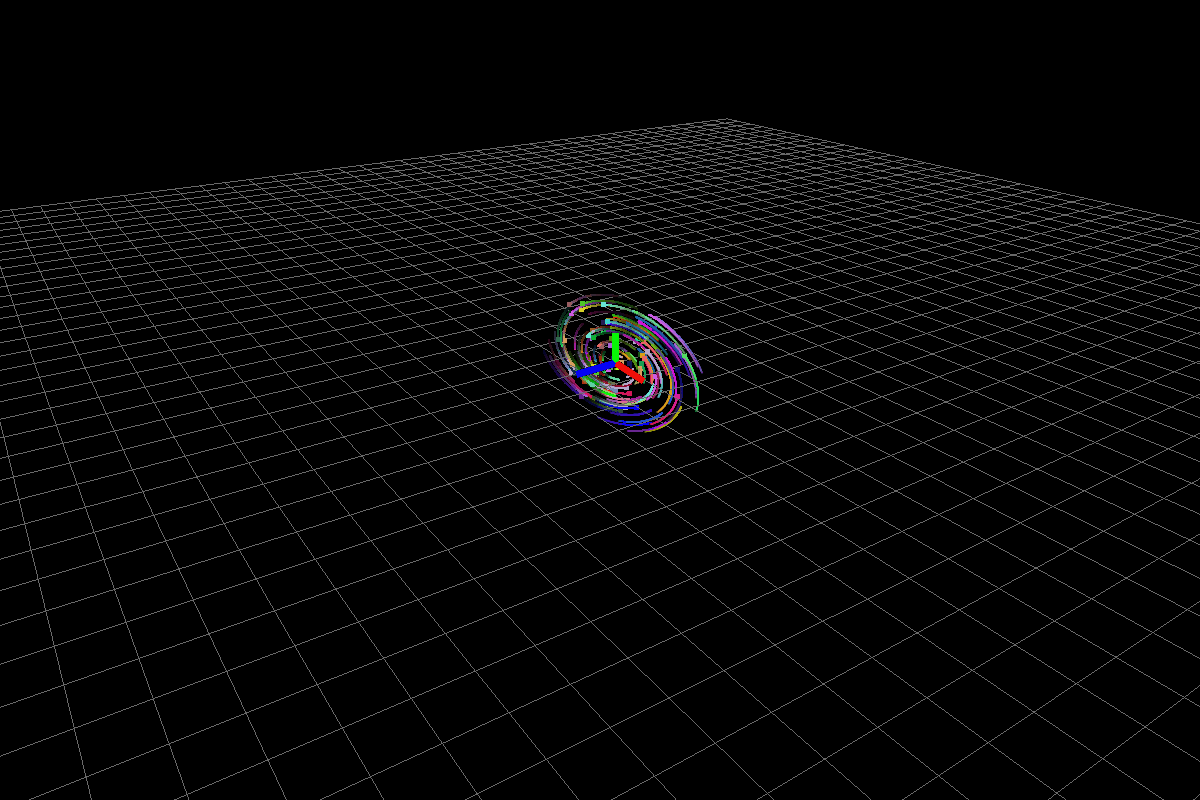Fig3: Stable system

Unstable system (with positive real part complex eigenvalues)

$A = \begin{bmatrix} 0 & -2 & 3 \\ 2 & 0 & -2 \\ 0 & 2 & -2 \\ \end{bmatrix}$

The above system has eigenvalues (-0.2,0) (0.2,2.22711) (0.2,-2.22711) .

Fig4: Unstable system